How to Know Which Error Propagation Formula to Use

For example because the area of a circle is proportional to the square of its diameter if you know the diameter with a relative precision of 5 percent you know the area with a relative precision of 10 percentFor example under certain assumptions the half-life t 12 of a drug in the body is related to the terminal elimination rate constant k e for the drug by the formula. You can use a very general simulation approach that can easily analyze how errors propagate through even the most complicated expressions involving any number of variables.

Propagation Of Uncertainty Rules For Estimating Uncertainty Isobudgets

Fit_params residuals rank s_values rcond nppolyfit x y 1 fullTrue poly_func nppoly1d fit_params x_unm The unmeasured x value y_unm poly_func x_unm The unmeasured x value.

. There is 01 cm uncertainty in the ruler used to measure r and h. However I note that if θ is given in terms of radians and degrees Δ θ will be scaled accordingly. The uncertainty in q is then q sµ q x1 x1 2.

RelX X jXj 1 Thus in the above example your 1cm uncertainty on your 589m measure-ment would turn into a relative error of 00016. This is the most general expression for the propagation of error from one set of variables onto another. Youll need to use a bit of calculus specifically the chain rule.

Example For a fair dice the probability distribution function is discrete for integers from 1 to. This expression will be used in the Uncertainty Analysis section of every Physical Chemistry laboratory report. Measure Density of Earth.

The formal mathematical proof of this is well. For independent random errors δx δy and δz. In your particular case when you estimate SE of C A B and you know σ A 2 σ B 2 N A and N B then.

For a measurement θ with uncertainty Δ θ the propagated error of the sine function is given by. In other words the absolute. S E C σ A 2 N A σ B 2 N B.

Indeed standard error of the mean is nothing else than standard deviation of your estimate of the mean so the math does not change. Unfortunately we will never know Px because it is impossible to satisfy N. If the result 𝑅 is a function of measurements where 𝑅.

This is when you compare the size of your error to the size of the original quantity1 The formula for relative error is. L Unphysical situations can arise if we use the propagation of errors results blindlyu Example. V p p2 cm3.

Applying the above equation allows for the derivation of Gaussian error propagation for any arbitrary function. θ Δ θ. N Using propagation of errors.

The purpose of these measurements is to determine q which is a function of x1xn. µ q xn xn 2 10501 8. I have two problems with this approach.

Independent and omit the covariance. So the error in the volume delivered. Error Propagation tutorialdoc Daley 2 10909 R i.

θ cos. Even easier you can go to a web page that does the error-propagation calculations for functions of one or two variables. N Let R 1 cm exact and L 10 05 cm.

Show activity on this post. SY 1m sqrt sm² A-Bm² sA² sB² Now I want to. 21 or equivalently Q jQj jnj x jxj 22 The second form is probably easier to remember.

There are standard errors given for A B and m sAsBsm. The volume delivered by a 100-mL graduated cylinder is. Qq q222 qx y z xy z.

Z fx y x y x y2. The fractional or percent uncertainty gets multiplied by jnjwhen you raise xto the nth power. Although the idea of error propagation may seem intimidating you have already been using it since your first chemistry class when you applied the rules for significant figures in calculations.

When the errors on x are uncorrelated the general expression simplifies to Σ i j f k n A i k Σ k x A j k displaystyle Sigma _ijfsum _knA_ikSigma _kxA_jk. Df dx f x 2 dy f y 2. If nis an exact number and Q xn then Q jnjxn 1 x.

You can use some simple error-propagation formulas for simple expressions. Each reading has an uncertainty of 002 mL according to the buret manufacturer. Best best best best qqxy z qqxy z.

I can perform a linear fit in Python pretty easily if I dont consider the error. Fxy f xy is something more complex like. Main formula for error propagation always use this formula.

3 assuming that Δ x and Δ y are both 1 in the last decimal place quoted. These rules are simplified versions of Eqn. General Formula for Error Propagation Wemeasure x1x2xn withuncertainties x1x2xn.

N If the error on V sV is to be interpreted in the Gaussian sense. Suppose we measure the volume of a cylinder. The propagation of error formula for Y fX Z ldots a function of one or more variables with measurements X Z ldots gives the following estimate for the standard deviation of Y.

I can calculate the standard error of Y by error-propagation as. General Formula for Error Propagation. SV pR2s L p2 cm3.

The general formula for the propagation of errors is then 𝑅𝑅 2 2𝑅 2 2 where. The error propagation formula then reduces to Hdf L2 i k jj f ÅÅÅÅÅÅÅÅÅÅÅ x dx y zz 2 i k jj f ÅÅÅÅÅÅÅÅÅÅÅ y dy y zz 2 where we use the notation dx to represent an uncertainty instead of sx because we use an estimated uncertainty instead of an observed variance. δδ δ δ.

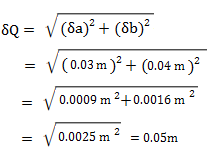
Error Propagation Propagation Of Uncertainty Statistics How To

Propagation Of Uncertainty Rules For Estimating Uncertainty Isobudgets

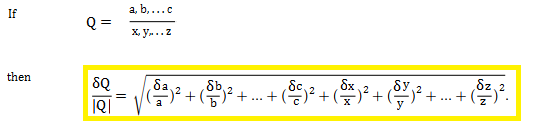
Error Propagation Propagation Of Uncertainty Statistics How To